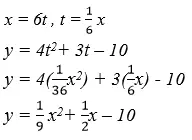Fungsi dalam matematika adalah suatu relasi yang menghubungkan setiap anggota x dalam suatu himpunan yang disebut daerah asal (domain) dengan suatu nilai tunggal f(x) dari suatu himpunan kedua yang disebut daerah kawan (codomain). Himpunan nilai yang diperoleh dari relasi tersebut disebut daerah hasil (range).
Jika ada dua himpunan, yaitu himpunan A dan himpunan B, maka suatu fungsi dari himpunan A ke himpunan B adalah suatu relasi yang khusus, yaitu relasi dimana setiap anggota A dikawankan dengan tepat satu anggota B. Artinya fungsi tidak akan pernah memiliki dua pasangan yang terdiri dari elemen pertama yang sama.
Penulisan fungsi dilambangkan dengan:
f∶x→y
dibaca “ f adalah fungsi dari x ke y”. Anggota y yang menjadi pasangan x oleh f disebut bayangan x dan ditulis
dibaca “ f dari x”.
Istilah – Istilah Dalam Fungsi Matematika
- Domain = daerah asal fungsi f (dilambangkan dengan Df)
- Kodomain = daerah kawan fungsi f (dilambangkan dengan Kf)
- Range = daerah hasil yang merupakan himpunan bagian dari kodomain. Range fungsi f (dilambangkan dengan Rf)
- Variabel = simbol yang melambangkan faktor tertentu
- Variabel bebas =tidak tergantung pada variabel lain
- Variabel terikat=tergantung pada variabel lain
- Koefisien = angka pembentuk fungsi yang terkait pada variabel dalam sebuah fungsi
- Konstanta = angka yang kadang-kadang menjadi pembentuk fungsi, tidak terikat pada variabel
Syarat Relasi Sebagai Fungsi Matematika
Jika notasi didefinisikan dengan f : A → B, maka maka dapat disimpulkan syaratnya adalah:
- Pertama, setiap anggota A mempunyai pasangan di B. Jika ada salah satu anggota A tidak memiliki pasangan di B, maka relasi tersebut bukan fungsi.
- Kedua, setiap anggota A dipasangkan dengan tepat satu anggota B. Jika anggota A memilik lebih dari satu pasangan maka relasi itu bukan fungsi. Syarat kedua ini tidak berlaku untuk sebaliknya, maksudnya jika syarat pertama dipenuhi anggota B boleh memiliki pasangan lebih dari satu di anggota A.
Cara Menyatakan Fungsi Pada Matematika
Fungsi dapat dinyatakan dalam diagram panah, diagram cartesius, dan pasangan berurutan. Lihat contoh dibawah ini:
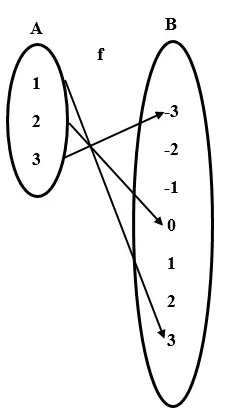
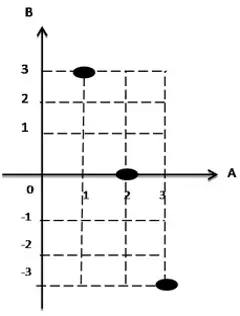
Misalkan A = {1, 2, 3} dan B = {-3, -2, -1, 0, 1, 2}. Jika fungsi f : A → B ditentukan dengan f(x) = 6 – 3x. Nyatakan dalam diagram panah, diagram cartesius, dan pasangan berurutan.
Penyelesaian :
- Diagram Panah
- Diagram Cartesius
- Himpunan Pasangan Berurutan
{(1, 3), (2, 0), (3, -3)}
Konsep Fungsi Pada Matematika
Konsep fungsi dalam matematikan umumnya diartikan sebagai pemetaan yang menghubungkan dua himpunan yang terpisah, yaitu daerah asal (domain) dan daerah hasil (range). Persamaan atau kesamaan akan terjadi apabila jumlah anggota himpunan yang berhubungan adalah sama, sehingga satu anggota daerah asal berhubungan hanya dengan satu anggota daerah hasil.
Sifat-Sifat Fungsi Matematika
- Fungsi Injektif
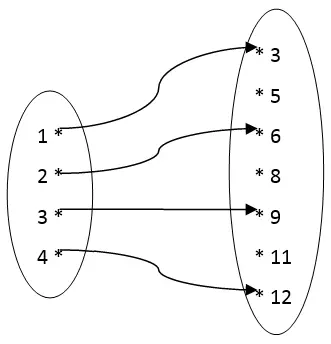
Suatu fungsi f dari himpunan x ke himpunan y dikatakan sebagai fungsi injektif apabila setiap anggota di x akan dipetakan pada anggota yang berbeda di B. Dapat disimpulkan bahwa f:x→y adalah fungsi injektif apabila x=y maka berakibat f(x)=f(y), jika x≠y berakibat f(x)≠f(y) atau ekuivalen.
Contoh:
f(x)= 3x
- Fungsi Surjektif
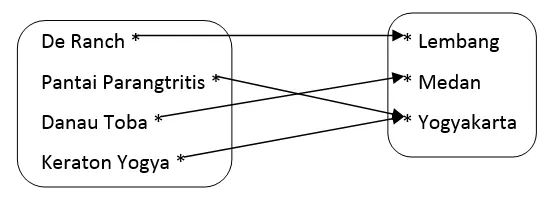
Suatu fungsi f dari himpunan x ke himpunan y dikatakan sebagai fungsi surjektif apabila f(x)= y yang berarti setiap anggota di y pasti merupakan peta dari sekurang-kurangnya satu anggota di x.
Contoh : f∶tempat wisata→daerah
- Fungsi Bijektif
Suatu fungsi f dari himpunan x ke himpunan y dikatakan sebagai fungsi surjektif apabila pemetaan f:x→y sedemikian rupa sehingga f merupakan fungsi yang injektif dan surjektif sekaligus.
Contoh: Jika suatu fungsi f:A→B merupakan fungsi injektif sekaligus fungsi surjektif, maka f adalah fungsi yang bijektif atau “A dan B berada dalam korespondensi satu-satu” seperti pada gambar berikut.
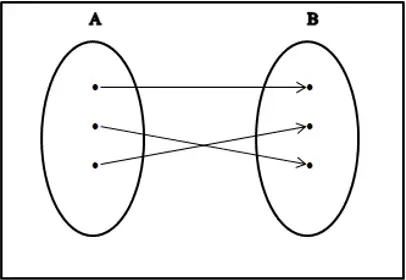
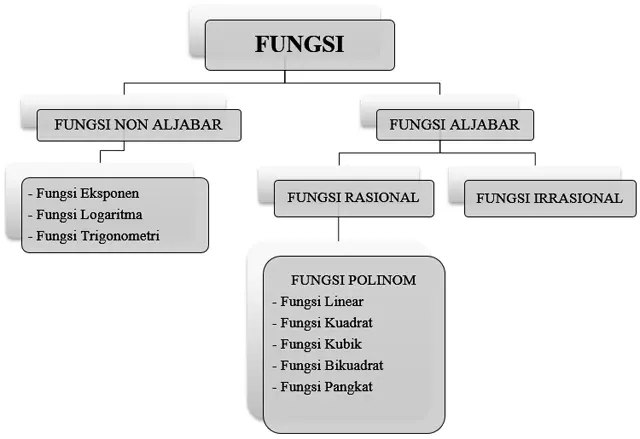
Jenis – Jenis Fungsi Matematika
Fungsi digolongkan menjadi beberapa jenis, lihat gambar bagan dibawah ini:
- Fungsi Non Aljabar
- Fungsi Eksponen adalah fungsi yang variabel bebasnya berupa pangkat dari suatu konstanta dalam persamaan fungsi tersebut.
Bentuk umum : y=ax
Grafik fungsi eksponen tidak memiliki titik potong pada sumbu x dan tidak memiliki nilai ekstrim.
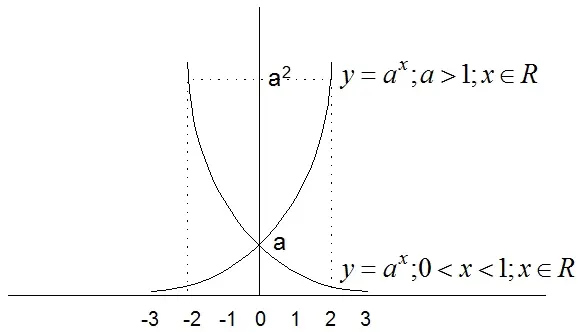
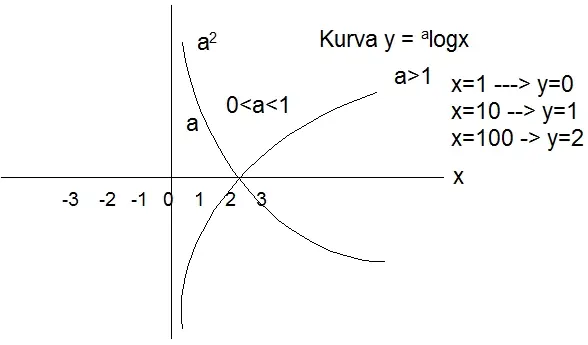
- Fungsi Logaritma adalah invers fungsi dari fungsi eksponen. Karena adanya hubungan kesetaraan sifat eksponen dan logaritma y = alog x = ax.
Bentuk umum : y = alog x
Grafik fungsi logaritma tidak memiliki titik potong pada sumbu y dan tidak memiliki nilai ekstrim
- Fungsi Trigonometri adalah fungsi yang variabel bebasnya berupa bilangan geometris, variabel x biasanya dinyatakan dalam radian (p radian = 1800). diantaranya :
y = sin x ; y = cos x ; y tan x; y = ctg x ; y = sec x ; dan y = cosec x
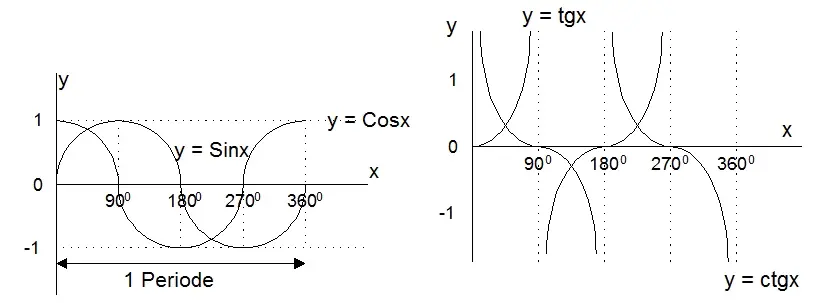
- Fungsi Aljabar
- Fungsi Rasional adalah fungsi yang pangkat tertinggi dari variabel bebasnya menjadi penentu identitasnya.
- Fungsi Polinom,variabel bebasnya mengandung banyak suku (polinom).
Bentuk umum : y = anx~ + … + a2x2 + a1x + a0 - Fungsi Linear, fungsi dengan pangkat tertingginya adalah satu.
Bentuk umum : y = a1x + a0
Grafiknya : - Fungsi Kuadrat, fungsi dengan pangkat tertingginya adalah dua.
Bentuk umum : y = a2x2 + a1x + a0
Contoh Grafik Parabola :
Setiap parabola memiliki satu titik puncak dengan 4 kemungkinan. Adapun rumus mencari titik puncak adalah
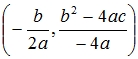
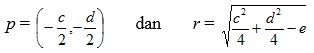
- Fungsi Kubik, fungsi dengan pangkat tertingginya adalah tiga.
Bentuk persamaan : y = a3x3 + a2x2 + a1x + a0
Grafiknya :
Fungsi kubik memiliki titik maksimum, titik minimum dan titik belok. Ada fungsi kubik yang tidak memiliki titik maksimum dan minimum, melainkan hanya titik belok.
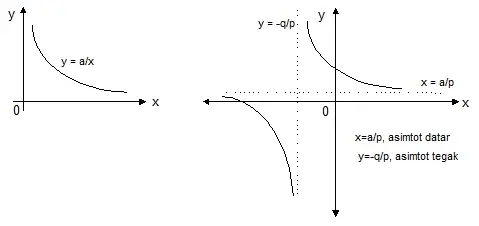
- Fungsi Pecah ( berderajat n )
Bentuk umum :Fungsi pecah istimewa yang sering diterapkan dalam ilmu ekonomi adalah y=ª/χ dimana a > 0
Grafiknya :
- Fungsi Pangkat, fungsi dengan variabel bebasnya berpangkat suatu bilangan riil dalam persamaannya.
Bentuk umum : y = xn - Fungsi Irasional adalah fungsi yang pada variabel bebasnya terdapat penarikan akar.
Bentuk umum :
Berdasarkan letak ruas variabel fungsi maka jenis fungsi dibedakan menjadi 3, yaitu :
- Fungsi Eksplisit
Fungsi dimana letak variabel bebas dan variabel terikatnya berada di ruas yang berbeda. Dengan kata lain variabel bebas dan terikat dipisahkan oleh tanda sama dengan. ditulis y = f(x), contoh y = 2x + 1
- Fungai Implisit
Fungsi dimana letak variabel bebas dan variabel terikat berada dalam satu ruas yang sama. Ditulis f(x,y) = 0, contoh 3x + 2y – 8 = 0
- Fungsi parameter
Fungsi dimana variabel bebas dan variabel terikat tidak berhubungan langsung tetapi menggunakan parameter / variabel bantu. Ditulis x = f(t) , y = f(t)
Contoh
Demikian pembahasan mengenai fungsi matematika dari pengertian hingga konsepnya. semoga membantu kalian, terimakasih.


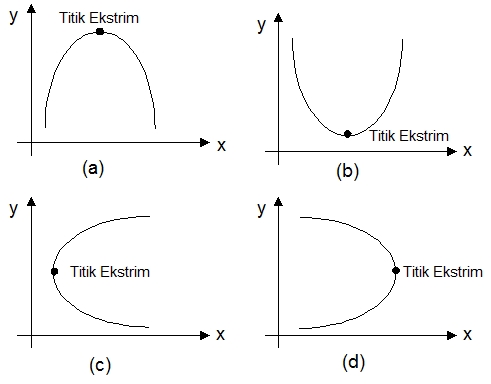 Setiap parabola memiliki satu titik puncak dengan 4 kemungkinan. Adapun rumus mencari titik puncak adalah
Setiap parabola memiliki satu titik puncak dengan 4 kemungkinan. Adapun rumus mencari titik puncak adalah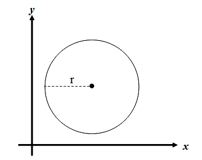
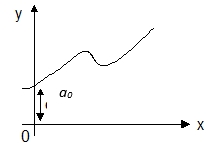 Fungsi kubik memiliki titik maksimum, titik minimum dan titik belok. Ada fungsi kubik yang tidak memiliki titik maksimum dan minimum, melainkan hanya titik belok.
Fungsi kubik memiliki titik maksimum, titik minimum dan titik belok. Ada fungsi kubik yang tidak memiliki titik maksimum dan minimum, melainkan hanya titik belok.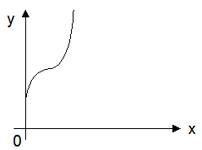
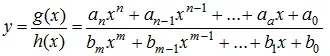 Fungsi pecah istimewa yang sering diterapkan dalam ilmu ekonomi adalah y=ª/χ dimana a > 0
Fungsi pecah istimewa yang sering diterapkan dalam ilmu ekonomi adalah y=ª/χ dimana a > 0