Angka dapat diperoleh dari mengukur dan membilang. Untuk mengetahui luas tanah perkebunan misalnya, maka harus dilakukan pengukuran. Sedangkan untuk mengetahui jumlah pohon yang tertanam di kebun maka diperoleh dengan cara membilang. Angka yang diperoleh dari hasil megukur disebut angka penting (berarti). Sedangkan angka hasil membilang disebut angka eksak (pasti).
Angka dapat diperoleh dari mengukur dan membilang. Untuk mengetahui luas tanah perkebunan misalnya, maka harus dilakukan pengukuran. Sedangkan untuk mengetahui jumlah pohon yang tertanam di kebun maka diperoleh dengan cara membilang. Angka yang diperoleh dari hasil megukur disebut angka penting (berarti). Sedangkan angka hasil membilang disebut angka eksak (pasti).
Angka penting terdiri dari angka pasti dan angka yang diragukan (angka taksiran). Angka taksiran pada angka penting (angka hasil pengukuran) terletak digit terakhir. Misalkan hasil pengukuran tebal buku menggunakan jangka sorong adalah 1,25 cm. Angka 1 dan 2 adalah angka pasti, sedangkan angka 5 adalah taksiran.
Gambar dibawah ini menunjukkan pengukuran sebuah benda dengan menggunakan mistar. Hasil pengukuran panjang benda tersebut pasti lebih dari 1,6 cm. Jika skala tersebut kita perhatikan lebih cermat, ujung logam berada kira-kira di tengah-tengah antara skala 1,6 cm dan 1,7 cm. Kalau kita mengikuti aturan penulisan hasil pengukuran hingga setengah skala terkecil, panjang logam dapat dituliskan 1,65 cm.
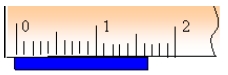
Angka terakhir (angka 5) merupakan angka taksiran, karena terbacanya angka tersebut hanyalah dari hasil menaksir atau memperkirakan saja. Sedangkan angka 1 dan 6 (pada 1,6 cm) merupakan angka pasti. Berarti hasil pengukuran 1,65 cm terdiri dari dua angka pasti, yaitu angka 1 dan 6, dan satu angka taksiran yaitu angka 5. Angka-angka hasil pengukuran yang terdiri dari satu atau lebih angka pasti dan satu angka taksiran disebut angka penting.
Jika ujung benda yang diukur berada pada skala 1,6 cm, hasil pengukuran harus ditulis dengan 1,60 cm bukan 1,6 cm. Penulisan angka nol pada 1,60 cm menunjukkan bahwa ketelitian pengukuran sampai 2 angka di belakang koma. Karena angka 0 pada 1,60 cm ini memiliki makna tertentu, maka angka nol pada 1,60 termasuk angka penting. Jadi 1,60 cm terdiri dari tiga angka penting, yaitu dua angka pasti (1 dan 6) dan satu angka taksiran (0).
Untuk mengidentifikasi apakah suatu angka hasil pengukuran termasuk angka penting atau bukan, dapat diikuti beberapa kriteria di bawah ini.
- Semua angka yang bukan nol merupakan angka penting.
- Angka nol diantara angka yang bukan nol adalah angka penting.
- Angka-angka nol awalan bukan angka penting.
- Pada angka yang memiliki nilai (pecahan) desimal, angka nol akhiran adalah angka penting.
- Pada angka yang tidak memiliki nilai (pecahan) desimal (puluhan, ratusan, ribuan), angka nol akhiran bisa merupakan angka penting atau tidak, tergantung informasi tambahan terkait ketelitian alat ukur yang digunakan. Atau dapat ditulis dengan notasi ilmiah agar jelas apakah angka-angka nol itu termasuk angka penting atau bukan.
Angka nol sering menimbulkan masalah dalam penentuan banyaknya angka penting. Contoh: pada hasil suatu pengukuran yang menunjukkan 0,0027 kg, hanya mengandung dua angka penting yaitu 2 dan 7, sedangkan pada pengukuran 0,00270 kg mempunyai 3 angka penting yaitu 2, 7, dan 0. Angka 0 dibelakang 7 termasuk angka penting, sedangkan dua nol didepan (sebelum) angka 27 bukan termasuk angka penting.
Demikian juga pada pengukuran yang menunjukkan hasil 2700 gram, kedua angka nol di kanan angka 7 bisa saja termasuk angka penting tetapi bisa juga tidak. Untuk menghindari masalah seperti itu, maka hasil pegukuran sebaiknya dinyatakan dalam notasi ilmiah. Dalam notasi ilmiah, semua angka yang ditampilan sebelum orde besar termasuk angka penting.
|
0,0027 kg |
2,7 x 10 –3 kg |
Mempunyai 2 angka penting yaitu 2 dan 7 |
|
2,70 x 10 –3 kg |
Mempunyai 3 angka penting yaitu 2,7, dan 0 |
|
|
1300 g |
1,3 x 10 3 g |
Mempunyai 2 angka penting yaitu 1 dan 3 |
|
1,30 x 10 3 g |
Mempnyai 3 angka penting yaitu 1,3, dan 0 |
|
|
1,300x 10 3 g |
Menpunyai 4 angka penting yaitu, 1,3, 0, dan 0 |
Dalam notasi ilmiah, hasil pengukuran dinyatakan sebagai:
a,…. X 10n
Keterangan rumus:
a adalah bilangan asli mulai dari 1 sampai dengan 9,
n disebut eksponen dan merupakan bilangan bulat.
Dalam persamaan itu, a,..disebut angka penting sedangkan 10n disebut orde besar.
Aturan Pembulatan
Jika kita melakukan perhitungan terhadap hasil pengukuran, misal penjumlahan, pengurangan, pengalian, atau pembagian, sehingga dihasilkan angka hasil perhitungan yang jumlah angka di belakang komanya melebihi ketelitian alat, maka kita perlu melakukan pembulatan. Adapun aturan pembulatannya adalah sebagai berikut.
Aturan 1. Jika angka pertama setelah angka yang akan kita pertahankan andalah angka 4 atau lebih kecil, angka itu dan seluruh angka di sebelah kananya ditiadakan. Angka terakhir yang dipertahankan tidak berubah.
Contoh 1 Aturan 1:
Hasil perhitungan 72,684, padahal ketelitian alat ukur yang digunakan hanya sampai dua angka dibelakang koma, maka dilakukan pembulatan menjadi 72,68 (4 adalah angka yang ditiadakan)
Contoh 2 Aturan 1:
Hasil perhitungan 1,00729, padahal ketelitian alat ukur yang digunakan hanya sampai tiga angka di belakang koma, maka dilakukan pembulatan menjadi 1,007 (29 adalah angka yang akan ditiadakan)
Aturan 2. Jika angka pertama setelah angka yang akan kita pertahankan adalah 5 atau lebih besar, angka itu dan seluruh angka di sebelah kananya ditiadakan. Angka terakhir yang dipertahankan ditambah dengan satu.
Contoh 1 Aturan 2:
Hasil perhitungan 1,046859, padahal ketelitian alat ukur yang digunakan hanya sampai tiga angka di belakang koma, maka dilakukan pembulatan menjadi 1,047 (8,5,9 adalah angka yang ditiadakan).
Contoh 2 Aturan 2:
Hasil perhitungan 26,02500, padahal ketelitian alat ukur yang digunakan hanya sampai dua angka di belakang koma, maka dilakukan pembulatan menjadi 26,03 (2, 5, 0, 0 adalah angka yang ditiadakan).
Perhitungan angka hasil pengukuran
Hasil operasi matematis yang diperoleh dari pengukuran tidak bisa lebih teliti daripada hasil pengukuran dengan ketelitian yang paling kecil. Jadi perhitungan tidak dapat menjadikan pengukuran menjadi lebih teliti.
Misal, pengukuran panjang sebuah benda diperoleh hasil 5,14 m dan 14, 8 m. Hasil pengukuran 5,14 m mengindikasikan bahwa mistar yang digunakan memiliki skala terkecil 0,1 m (karena 4 sebagai angka taksiran). Sedangkan, hasil pengukuran 14,8 m mengindikasikan bahwa mistar yang digunakan memiliki skala terkecil 1m, sehingga angka 8 dalam 14,8 m adalah angka taksiran.
Jika kedua hasil pengukuran dijumlahkan, maka hasil penjumlahan ini hanya boleh ditulis sampai satu angka di belakang koma, yaitu sama dengan hasil pengukuran yang ketelitiannya paling rendah (paling kurang teliti). Oleh karena itu, hasil penjumlahan 19,94 m ditulis menjadi 19,9 m.
Contoh soal angka hasil pengukuran
- Jumlahkan 123,217 g dengan 2,42 g
Penyelesaian:
123,217 g (7 adalah angka taksiran, angka ketiga di belakang koma)
2,42 g (2 adalah angka taksiran, angka kedua di belakang koma)
123,217 g + 2,42 g = 125,637 g dibulatkan menjadi 125,63 g (3 adalah angka taksiran, angka kedua di belakang koma)
- Kurangi 2,74 x 104 g dengan 5,950 x 103 g
Penyelesaian:
27,4 x 103 g (4 adalah angka taksiran)
5,950 x 103 g (0 adalah angka taksiran)
27,4 x 103 g – 5,950 x 103 g = 21,45 x 103 g dibulatkan dan ditulis menjadi 21,5 x103 g =
2,15 x104 g (5 angka taksiran)
- Kalikan 3,22 m dengan 2,1 m
Penyelesaian:
3,22 m (mempunyaai 3 angka penting)
2,1 m (mempunyai 2 angka penting)
3,22 m x 2,1 m = 6,762 m2 = 6,8 m2 (hasil harus sama dengan komponen yang mempunyai angka penting paling sedikit)
- Bagilah 4,554 x 105 kg dengan 3,0 x 105 m3
Jawaban :
4,554 x 105 kg (mempunyai 4 angka penting)
3,0 x 105 m3 (mempunyai 2 angka penting)
4,554 x 105kg : 3,0 x 105 m3 = 1,518 kg/m3 = 1,5 kg/m3 (hasil harus sama dengan komponen yang mempunyai angka penting paling sedikit)