Pada sekolah menengah kita telah mempelajari bagaimana menjumlahkan vektor-vektor yang dapat membantu kita untuk menggambarkan gerak proyektil dan gerak melingkar. Gerak dari sebuah proyektil dapat digambarkan melalui penjumlahan vektor kecepatan, sedangkan pada gerak melingkar kita menemui pengurangan vektor kecepatan dan penjumlahan vektor percepatan.
Penjumlahan vektor secara khusus digunakan dalam menentukan apa yang diketahui sebagai posisi dan kecepatan relatif. Mulai saat ini dan seterusnya dalam setiap pembahasan teori relativitas kita akan menggunakan bahwa semua kecepatan adalah ”relatif”. Oleh karena pada kenyataannya semua besaran-besaran vektor adalah relatif terhadap sistem koordinat di mana besaran-besaran vektor tersebut diamati dan diukur.
Dalam menentukan koordinat dari benda-benda yang bergerak atau diam terhadap benda lainnya, kita harus menyatakan di mana letaknya (atau kedudukannya) dan pada saat waktu kapan objek itu berada. Untuk mengetahui di mana kedudukan sebuah objek kita harus mengukur posisi relatifnya terhadap sesuatu.
Maka, kita memerlukan titik acuan di mana kita dapat mendefinisikan posisi dari objek tersebut. Pertama kita memilih sebuah titik yang dinamakan dengan titik asal koordinat, selanjutnya kita menentukan posisi dari objek tersebut dari titik ini. Misalnya, posisi objek adalah berjarak x ke arah Barat, berjarak y ke arah Selatan dan berjarak z ke arah Utara diukur dari titik asal. Kita juga membutuhkan sebuah jam sedemikian sehingga kita dapat menentukan pada waktu t kapan objek berada pada posisi tersebut.
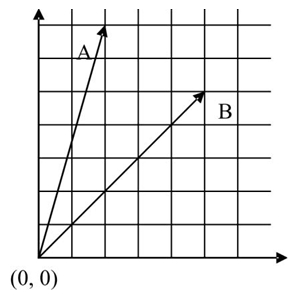
Sebagai contoh, bagaimana kita menghitung kedudukan relatif dari benda A dan B yang diberikan oleh Gambar Menentukan kedudukan relatif dibawah ini. Maka jika kita memilih (0,0) sebagai titik asal koordinat,
Menentukan Kedudukan Relatif Teori Relativitas
- Posisi A relatif terhadap titik asal adalah (x, y) = (2, 7)
- Posisi B relatif terhadap titik asal adalah (x, y) = (5, 5)
- Posisi A relatif terhadap B adalah (x, y) = (-3, 2)
- Posisi B relatif terhadap A adalah (x, y) = (3, -2)
Jadi, posisi dari sebuah objek bergantung pada posisi objek yang lain, posisinya adalah relatif.
Gambar Menentukan kedudukan relatif
Oleh karena posisi adalah besaran-besaran relatif maka turunan waktu dari besaran ini, yaitu kecepatan juga merupakan besaran relatif. Kecepatan relatif biasanya digunakan untuk menyatakan sebuah kecepatan yang diukur relatif terhadap sebuah sistem koordinat.
Sistem koordinat dari kecepatan itu sendiri, bergerak relatif terhadap suatu sistem koordinat tetap. Kita akan membahas sistem koordinat lebih jauh pada subpokok bahasan setelah ini.
Misalkan sebuah kendaraan patroli mengejar pada kecepatan 120 km/jam sebuah mobil yang melaju di jalan raya 100 km/jam. Vektor kecepatan untuk polisi yang berada di dalam kendaraan patroli (P) relatif terhadap tanah (G) akan tampak sebagai berikut.
Vektor kecepatan dari orang di dalam mobil yang dikejar (C), berada dalam mobilnya, relatif terhadap tanah.
Dan bila kita gabungkan keduanya kecepatan relatif terhadap tanah:
Oleh karena itu, vektor kecepatan dari kendaraan patroli relatif terhadap mobil akan tampak:
Dengan kata lain, kendaraan patroli mendekati mobil dengan laju 20 km/jam. Atau orang yang berada di dalam mobil bila dia melihat melalui cermin mobilnya, akan tampak polisi mendekati dirinya. Sebaliknya, polisi melihat orang itu datang ke arahnya dengan laju 20 km/jam. Vektor untuk mobil relatif terhadap kendaraan patroli adalah:
Contoh ini memberikan gambaran suatu cara untuk menyelesaikan permasalahan kecepatan relatif:
- Perlakukan besaran-besaran vektor dengan benar.
- Gambar masing-masing vektor dengan skala yang sesuai, nyatakan objek yang bergerak pada ujung anak panah dan objek ini bergerak relatif terhadap apa, nyatakan pada titik pangkalnya.
- Titik pangkal dan ujung dari vektor yang diberikan, menentukan titik- titik dalam sebuah ruang vektor (contoh ruang vektor adalah ruang vektor kecepatan).
- Lukiskan vektor-vektor di antara titik-titik dalam ruang vektor untuk menentukan suatu kecepatan relatif.
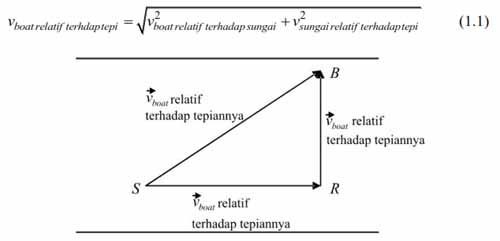
Misalnya, kita meninjau sebuah boat (B) dikayuh menyeberangi suatu aliran sungai (R), akan bergerak secara diagonal relatif terhadap tepian dari sungai (S) seperti ditunjukkan pada Gambar 1.2. Kita meninjau boat bergerak tegak lurus dengan sungai, sedangkan air sungai bergerak sejajar dengan tepian sungai. Bagi seseorang yang melihat boat dari tepi sungai, boat akan bergerak diagonal, yaitu jumlah vektor dari dua buah gerak yang tegak lurus.
Besarnya kecepatan boat vboat relatif terhadap tepian sungai adalah:
Gambar diatas menjelaskan bahwa dua buah gerak saling tegak lurus–boat bergerak relatif terhadap sungai dan sungai relatif terhadap tepi, menghasilkan sebuah perpindahan diagonal relatif terhadap tepian sungai.
Perlu dipahami, dalam membuat suatu diagram vektor untuk kasus-kasus seperti di atas, Anda harus membuat kerja Anda lebih mudah dengan memilih sumbu-sumbu sejajar, misalnya sumbu sejajar dengan salah satu dari vektor.
