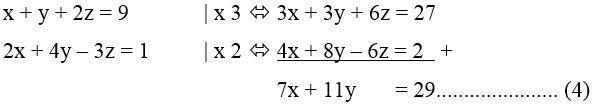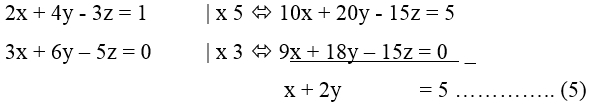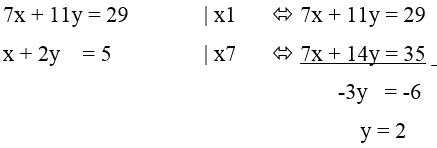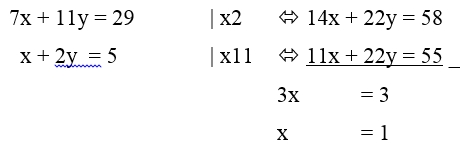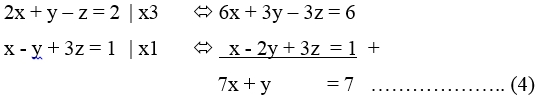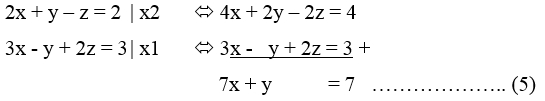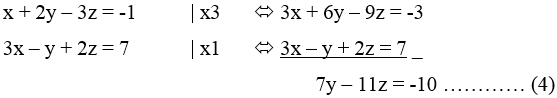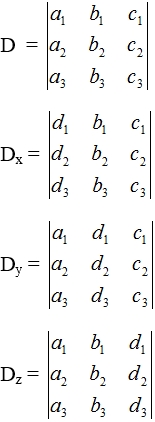Sistem Persamaan Linear Tiga Variabel adalah sistem persamaan yang terdiri dari Tiga Variabel atau Peubah. Banyak permasalahan dalam kehidupan nyata yang menyatu dengan fakta dan lingkungan budaya kita terkait dengan sistem persamaan linier. Permasalahan-permasalahan tersebut dapat kita susun model matematikanyauntuk menemukan penyelesaiannya. Model matematika tersebut, akan dijadikan bahan abstraksi untuk membangun konsep sistem persamaan linier tiga variabel.
Dalam kehidupan sehari-hari terdapat banyak masalah yang berkaitan dengan sistem persamaan linear tiga variable matematika. Untuk menyelesaikannya, cara yang harus dilakukan adalah merubah dahulu pernyataan-pernyataan pada masalah atau soal ke dalam bentuk suatu sistem persamaan-persamaan linear. Bentuk suatu sistem persamaan-persamaan linear tersebut merupakan model matematika yang kita cari himpunan penyelesaianya.
Bentuk Umum Sistem Persamaan Linear Tiga Variabel Matematika (SPLTV):
Bentuk umum SPLTV x, y, dan z dapat ditulis sebagai berikut:
a1x + b1y + c1z = d1
a2x + b2y + c2z = d2
a3x + b3y + c3z = d3
dengan a1, a2, a3, b1, b2, b3, c1, c2, c3, d1, d2, d3, ∈ R
Persamaan a1x + b1y + c1z = d1, a2x + b2y + c2z = d2, dan a3x + b3y + c3z = d3 merupakan persamaan di R3. Ketiga bidang tersebut dapat saling berpotongan di sebuah titik, sebuah garis, atau tidak berpotongan.
- Jika tiga bidang berpotongan dan perpotongannya berupa titik, maka SPLTV tersebut mempunyai satu anggota dalam himpunan penyelesaiannya (mempunyai penyelesaian tunggal), yaitu titik potong tersebut.
Dari gambar di atas terlihat, bahwa ketiga bidang bertemu (berpotongan) di satu titik, yaitu titik (x1, y1, z1). Jadi titik (x1, y1, z1) merupakan penyelesaian tunggal dari sistem persamaan linear tiga variabel tersebut.
- Jika tiga bidang berpotongan dan perpotongannya berupa garis, maka SPLTV tersebut mempunyai tak hingga banyak penyelesaian, yaitu titik-titik pada garis potong ketiga bidang tersebut. Terlihat pada gambar di atas, bahwa ketiga bidang berpotongan pada satu garis. Jadi titik-titik pada garis berpotongan merupakan penyelesaian dari SPLTV tersebut. Dengan kata lain SPLTV tersebut mempunyai tak hingga banyak anggota dalam himpunan penyelesaiannya (mempunyai lebih dari satu penyelesaian).
- Jika ketiga bidang tidak berpotongan sama sekali, maka SPLTV tersebut dapat digambarkan ke dalam tiga kemungkinan berikut ini. Terlihat pada gambar di atas bahwa, ketiga bidang tidak mempunyai titik atau garis potong. Dengan kata lain SPLTV ini tidak mempunyai anggota dalam himpunan Penyelesaiannya (himpunan Penyelesaiannya adalah himpunan kosong).
Secara aljabar, penyelesaian SPLTV dapat dicari dengan beberapa cara/metode antara lain:
-
- Metode substitusi
- Metode gabungan/kombinasi eliminasi dan substitusi
- Metode determinan
Menyelesaikan Sistem Persamaan Linear Tiga Variabel Matematika SPLTV dengan Metode Substitusi
Untuk menentukan penyelesaian/himpunan penyelesaian SPLTV dengan metode substitusi, langkah-langkahnya sebagai berikut:
- Pilihlah salah satu persamaan yang paling sederhana, kemudian nyatakan x sebagai fungsi y dan z, atau y sebagai fungsi x dan z, atau z sebagai fungsi x dan y.
- Substitusikan x atau y atau z yang diperoleh pada langkah pertama (1) ke dalam dua persamaan yang lainnya sehingga diperoleh SPLDV.
- Selesaikan SPLDV yang diperoleh pada langkah kedua (2)
Contoh:
1. Tentukan penyelesaian SPLTV berikut dengan substitusi
x + y + 2x = 9 ……….. (1)
2x + 4y – 3z = 1 …….. (2)
3x + 6y – 5z = 0 …….. (3)
Jawab:
Dari persamaan (1), kita dapatkan x = 9 – y – 2z ……….. (4)
Persamaan (4) disubstitusikan ke persamaan (2) dan (3)
2(9 – y – 2z) + 4y – 3z = 1
⇔2y – 7 z = -17 ………………………………………………. (5)
Dan
3(9 – y – 2z) + 6 – 5z = 0
⇔3y – 11z = -27 ……………………………………………….(6)
Sehingga diperoleh SPLTV berikut ini.
2y – 7z = -17 ………………………………………………… (5)
3y – 11z = -27 ……………………………………………….. (6)
Selanjutnya, kita dapat mencari nilai y dan z dengan cara substitusi seperti pada SPLDV.
Dari persamaan (5) diperoleh:Substitusi persamaan (7) ke persamaan (6)
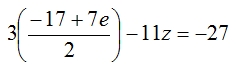
⇔-z = -3
⇔z = 3
Kemudian nilai z = 3 disubstitusikan ke persamaan (7), diperoleh nilai y = 2
Substitusikan y = 2 dan z=3 ke persamaan (4) diperoleh nilai x= 1.
Jadi SPLTV tersebut mempunyai penyelesaian tunggal yaitu (1,2,3) atau Himpunan Penyelesaiannya adalah {(1,2,3)}.
2. Tentukan penyelesaian dari SPLTV dengan substitusi
2x + y – z = 2 ………… (1)
x – 2y + 3z = 1 ……….. (2)
3x – y + 2z = 3 ……….. (3)
Jawab:
Misalkan substitusi dimulai pada variabel z terlebih dahulu (persamaan yang paling sederhana).
Dari persamaan (1) diperoleh: z = 2x + y – 2 …………….. (4)
Persamaan (4) disubstitusikan ke persamaan (2) dan (3) diperoleh:
x – 2y + 3(2x + y – 2) = 1
⇔7x + y = 7 ………………………………………………….. (5)
Dan
x – y + 2(2x + y – 2) = 3
⇔ 7x + y = 7 …………………………………………………. (6)
Persamaan (5) sama dengan persamaan (6), sehingga dari kedua persamaan ini dapat kita peroleh nilai satu peubah sebagai fungsi dari peubah yang lain, misalnya:
y = 7 – 7x ………………………………………………………. (7)
Substitusikan persamaan (7) ke persamaan (4), maka diperoleh:
z = 2x + (7 – 7x) – 2
z = -5x + 5
Jadi, penyelesaian dari SPLTV tersebut adalah:
x = x
y = 7 – 7x
z = 5 – 5x
Penyelesaian dari SPLTV ini banyak sekali, tergantung pada nilai x yang kita tentukan, misalnya.
- Jika x = 1, maka y = 0 dan z = 0 atau
- Jika x = 0, maka y = 7 dan z = 5 atau
- Jika x = -1, maka y = 14 dan z = 10 dan seterusnya
Dengan kata lain SPLTV ini mempunyai tak hingga banyak anggota dalam Himpunan Penyelesaiannya.
Cara lain
Persamaan (5) sama dengan persamaan (6): berarti persamaan yang satu merupakan kelipatan dari persamaan yang lain, maka himpunan penyelesaiannya mempunyai tak hingga banyak anggota.
3. Tentukan penyelesaian dari SPLTV dengan substitusi
x + 2y – 3z = -1 …………………………………………………. (1)
3x – y + 2z = 7 …………………………………………………… (2)
5x + 3y – 4z = 2 …………………………………………………. (3)
Jawab:
Misalkan substitusi dimulai pada variabel x, dari persamaan (1) diperoleh:
x = -2y + 3z – 1 ……………………………………………….. (4)
Persamaan (4) disubstitusikan ke persamaan (2) dan (3) diperoleh:
3(-2y + 3z – 1) – y + 2z = 7
⇔-7y + 11z = 10 …………………………………………….. (5)
dan
5(-2y + 3z – 1) + 3y – 4z = 2
⇔-7y + 11z = 7 ………………………………………………. (6)
Persamaan (5) dan (6) menyatakan bahwa SPLDV tersebut tidak konsisten sehingga SPLTV tidak mempunyai penyelesaian.
Menyelesaikan Sistem Persamaan Linear Tiga Variabel Matematika SPLTV dengan Metode Eliminasi Substitusi
Untuk menentukan penyelesaian/himpunan penyelesaian SPLTV dengan metode eliminasi, langkah-langkahnya sebagai berikut:
- Eliminasi salah satu variabel x atau y atau z sehingga diperoleh Sistem Persamaan Linear Dua Variabel (SPLTV).
- Selesaikan SPLTV yang diperoleh dari langkah (1)
- Substitusikan nilai-nilai variabel yang diperoleh pada langkah-langkah 2 ke dalam salah satu persamaan semula untuk mendapatkan nilai variabel yang lainnya.
Contoh:
1. Tentukan penyelesaian dari SPLTV berikut dengan Eliminasi
x + y + 2z = 9 ………………. (1)
2x + 4y – 3z = 1 ……………. (2)
3x + 6y – 5z = 0 ……………. (3)
Eliminasi z dari persamaan (1) dan (2) sehingga diperoleh:
Eliminasi z dari persamaan (2) dan (3) sehingga diperoleh persamaan:
Dari persamaan (4) dan (5) diperoleh SPLDV, yaitu:
Eliminasi x pada persamaan (4) dan (5) diperoleh nilai y
Eliminasi y pada persamaan (4) dan (5) diperoleh nilai x
Substitusikan nilai x = 1 dan y = 2 ke persamaan yang paling sederhana (misal persamaan (1)) sehingga diperoleh nilai z
x + y + 2x = 9
⇔1 + 1 + 2z = 9
2z = 6
z = 3
Penyelesaian SPLTV tersebut adalah x = 1, y = 2, z = 3 atau (1, 2, 3). Sedangkan himpunan penyelesaiannya {(1,2,3)}
2. Tentukan penyelesaian dari SPLTV berikut dengan Eliminasi
2x + y – z = 2 ……………… (1)
x – 2y + 3x = 1 ……………. (2)
3x – y + 2z = 3 …………….. (3)
Eliminasi z dari persamaan (1) dan (2) diperoleh persamaan (4)
Eliminasi z dari persamaan (1) dan (3) diperoleh persamaan (5)
Terlihat bahwa persamaan (4) sama dengan persamaan (5) sehingga kita peroleh nilai satu variabel yang merupakan fungsi dari variabel yang lain, yaitu y = 7 – 7x.
Substitusikan nilai y = 7 – 7x ke persamaan (1), diperoleh:
2x + (7 – 7x) – z = 2
⇔ z = -5x + 5
Penyelesaian SPLTV tersebut adalah:
x = x
y = -7x + 7
z = -5x + 5
Dengan kata lain, SPLTV ini mempunyai banyak penyelesaian tergantung pada nilai variabel x yang kita tentukan.
Cara Lain:
Persamaan (4) sama dengan persamaan (5), berarti persamaan yang satu mrupakan kelipatan dari persamaan yang lain, maka himpunan penyelesaiannya mempunyai tak hingga banyak anggota.
Tentukan penyelesaian SPLTV berikut dengan Eliminasi
x + 2y – 3z = -1 …………. (1)
3x – y + 2z = 7 …………. (2)
5x + 3y – 4z = 2 ………… (3)
Eliminasi x dari persamaan (1) dan (2) diperoleh persamaan (4)
Eliminasi x dari persamaan (1) dan (3) diperoleh persamaan (5)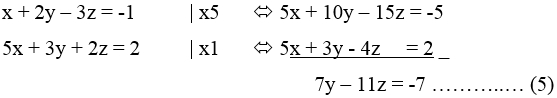
Menyelesaikan SPLTV Matematika dengan Metode Determinan
Jika bentuk umum SPLTV:
a1x + b1y + c1z = d1 …………………………………………………… (1)
a2x + b2y + c2z = d2 …………………………………………………… (2)
a3x + b3y + c3z = d3 …………………………………………………… (3)
maka:
Penyelesaian SPLTV tersebut adalah:
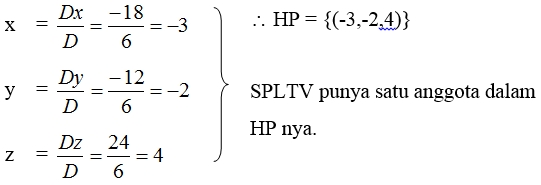
x = Dx/D
y = Dy/D
z = Dz/D
- Jika D ≠ 0, Dx ≠ 0, Dy ≠ 0, Dz ≠ 0, maka SPLTV tersebut mempunyai satu anggota dalam himpunan penyelesaiannya.
- Jika D = 0, Dx ≠ 0, Dy ≠ 0, Dz ≠ 0, maka SPLTV tersebut tidak memiliki anggota dalam himpunan penyelesaiannya.
- Jika D = 0, Dx = 0, Dy = 0, Dz = 0, maka SPLTV tersebut mempunyai tak hingga banyak anggota dalam himpunan penyelesaiannya.
Contoh:
Dengan metode Determinan, tentukan himpunan penyelesaian dari SPLTV:
x + y + z = 1
x + 2y + 3z = 5
3x + 2y – z = -9
Jawab :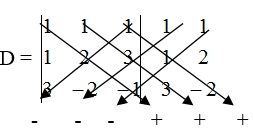
= 6
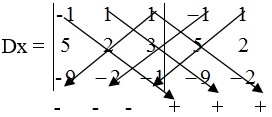
= 18
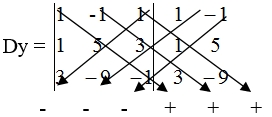
= -126
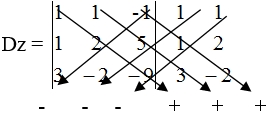
= 24
Berdasarkan contoh diatas dapat dituliskan definisi himpunan penyelesaian sistem persamaan linear sebagai “Himpunan penyelesaian sistem persamaan linear tiga variabel adalah suatu himpunan tripel terurut (x, y,z) yang memenuhi setiap persamaan linear pada sistem persamaan“. Penyelesaian sistem persamaan linear tiga variabel matematika dapat diselesaikan dengan metode eliminasi, substitusi, dan determinan. Itulah beberapa cara penyelesaian sistem persamaan tiga variabel yang sudah disajikan beserta contoh cara menyelesaikannya. Semoga bermanfaat bagi kalian.


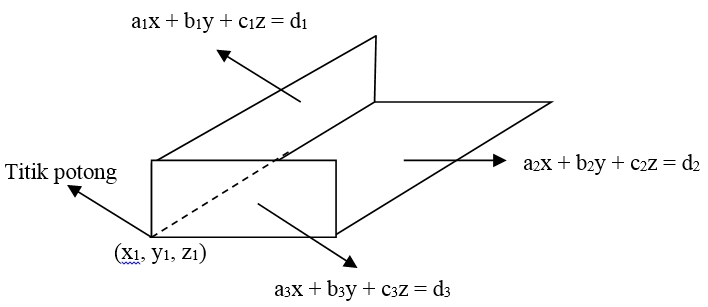 Dari gambar di atas terlihat, bahwa ketiga bidang bertemu (berpotongan) di satu titik, yaitu titik (x1, y1, z1). Jadi titik (x1, y1, z1) merupakan penyelesaian tunggal dari sistem persamaan linear tiga variabel tersebut.
Dari gambar di atas terlihat, bahwa ketiga bidang bertemu (berpotongan) di satu titik, yaitu titik (x1, y1, z1). Jadi titik (x1, y1, z1) merupakan penyelesaian tunggal dari sistem persamaan linear tiga variabel tersebut.