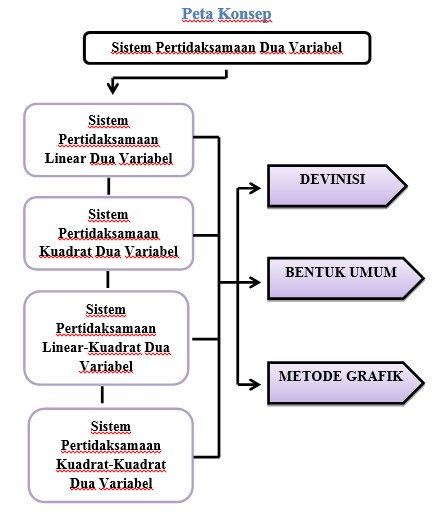
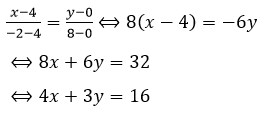- Pertidaksamaan Linear Dua Variabel
Pertidaksamaan linear dua variabel adalah suatu pertidaksamaan yang di dalamnya memuat dua variabel dan masing-masing variabel itu berderajat satu. Pertidaksamaan linear dua variabel ax+by≤c atau ax+by≥c dapat diselesaikan dengan langkah-langkah sebagai berikut.
- Buat grafik garis ax+by=c
-
- Tentukan titik potong garis ax+by=c dengan sumbu X dan sumbu Y.
- Tarik garis lurus melalui kedua titik tersebut.
- Uji titik
Ambil sembarang titik uji P(x_1,y_1) yang terletak di luar garis ax+by=c dan hitunglah nilai ax_1+by_1, kemudian bandingkan nilai ax_1+by_1 dengan nilai c.
-
- Jika ax_1+by_1≤c, bagian belahan bidang yang memuat titik P(x_1,y_1) ditetapkan sebagai daerah himpunan penyelesaian dari pertidaksamaan ax+by≤c.
- Jika ax_1+by_1≥c, bagian belahan bidang yang memuat titik P(x_1,y_1) ditetapkan sebagai daerah himpunan penyelesaian dari pertidaksamaan ax+by≥c.
- Sistem Pertidaksamaan Linear Dua Variabel
Sistem pertidaksamaan linear dua variabel adalah sistem pertidaksamaan yang terbentuk dari dua atau lebih pertidaksamaan linear dua variabel dengan variabel-variabel yang sama.
Contoh: 4x-2y≤5 dan 2x+5y≥1
Daerah atau grafik himpunan penyelesaian dari sistem pertidaksamaan linear dengan dua variabel merupakan irisan dari masing-masing daerah himpunan penyelesaian pertidaksamaan linear yang membentuknya.
- Contoh Soal dan Alternatif Penyelesaian Pertidaksamaan Linear Dua Variabel
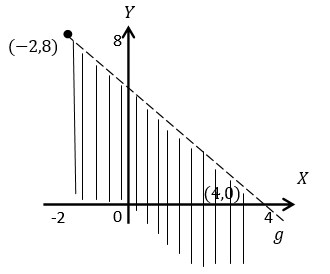
- Tentukan pertidaksamaan linear dua variabel yang memenuhi daerah yang diarsir pada gambar berikut!
Alternatif Penyelesaian
Garis g melalui titik (4,0) dan (-2,8), persamaannya adalah:
Ambil titik uji P(0,0) pada daerah yang diarsir, sehingga diperoleh: 4(0)+3(0)=0<16
Karena garis g putus-putus maka titik-titik pada garis 4x+3y=16 bukan penyelesaian dari pertidaksamaan.
Jadi, daerah yang diarsir merupakan himpunan penyelesaian dari pertidaksamaan linear dua variabel 4x+3y<16.
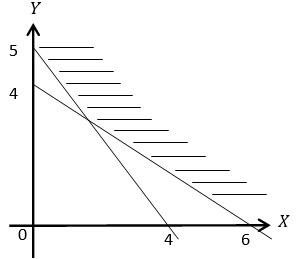
- Tentukan sistem pertidaksamaan linear yang daerah penyelesaiannya adalah daerah yang diarsir pada gambar berikut!
Alternatif Penyelesaian
Daerah yang diarsir di sebelah kanan sumbu Y dan di atas sumbu X berarti x≥0 dan y≥0.
Persamaan garis melalui titik (4,0) dan (0,5) adalah:
x/4+y/5=1⟺5x+4y=20
Ambil P(0,6) pada daerah penyelesaian sehingga diperoleh:
5(0)+4(6)=24 jadi,
5x+4y≥20 .
Persamaan garis melalui titik (6,0) dan (0,4) adalah:
x/6+y/4=1⟺4x+6y=24
⟺2x+3y=12
Ambil P(0,7) pada daerah penyelesaian sehingga diperoleh:
2(7)+3(0)=14 jadi,
2x+3y≥12.
Jadi, sistem pertidaksamaan linear dari daerah yang diarsir adalah:
x≥0;y≥0;5x+4y≥20;2x+3y≥12.