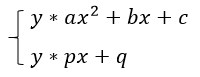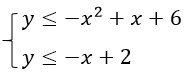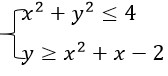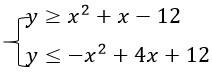Sistem Pertidaksamaan Kuadrat Dua Variabel – Matematika

Pertidaksamaan kuadrat dua variabel adalah pertidaksamaan yang memuat dua variabel dengan derajat tertinggi dua. Penyelesaian pertidaksamaan kuadrat dua pada dasarnya sama dengan penyelesaian pertidaksamaan linear dua variabel.

1. Pertidaksamaan Kuadrat Dua Variabel

Pertidaksamaan kuadrat dua variabel ax^2+by^2+cxy+dx+ey+f≤0 atau ax^2+by^2+cxy+dx+ey+f≥0 dapat diselesaikan dengan langkah-langkah sebagai berikut.

a. Buat kurva ax^2+by^2+cxy+dx+ey+f=0

b. Uji titik

Ambil sembarang titik uji P(x_1,y_1) yang terletak di luar kurva ax^2+by^2+cxy+dx+ey+=0 dan hitunglah nilai ax_1^2+by_1^2+cx_1 y_1+〖dx〗_1+ey_1+f, kemudian bandingkan nilai ax_1^2+by_1^2+cx_1 y_1+〖dx〗_1+ey_1+f dengan 0.

• Jika ax_1^2+by_1^2+cx_1 y_1+〖dx〗_1+ey_1+f≤0, bagian belahan bidang yang memuat titik P(x_1,y_1) ditetapkan sebagai daerah himpunan penyelesaian dari pertidaksamaan ax_1^2+by_1^2+cx_1 y_1+〖dx〗_1+ey_1+f≤0.
• Jika ax_1^2+by_1^2+cx_1 y_1+〖dx〗_1+ey_1+f≥0, bagian belahan bidang yang memuat titik P(x_1,y_1) ditetapkan sebagai daerah himpunan penyelesaian dari pertidaksamaan ax_1^2+by_1^2+cx_1 y_1+〖dx〗_1+ey_1+f≥0.

Masalah dan Alternatif Penyelesaian Pertidaksamaan Kuadrat Dua Variabel

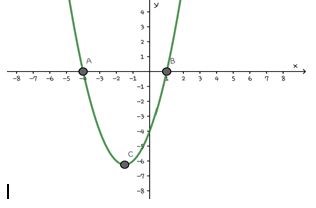
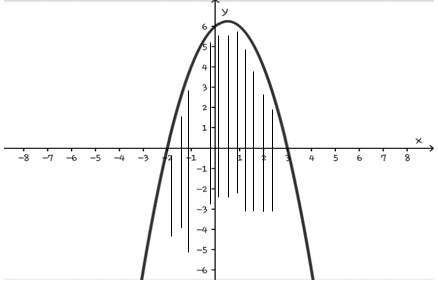
1. Tentukan daerah himpunan penyelesaian dari pertidaksamaan y≥x^2+3x-4!

Alternatif Penyelesaian Pertidaksamaan Kuadrat Dua Variabel

1. Menggambar grafik y=x^2+3x-4

y=x^2+3x-4 mempunyai nilai a=1 sehingga grafik terbuka ke atas.

Menentukan titik potong grafik dengan sumbu X→y=0

x^2+3x-4=0

⇔(x+4)(x-1)=0

⇔x=-4 atau x=1

Jadi, titik potong dengan sumbu X adalah (-4,0) dan (1,0).

Menentukan titik potong grafik dengan sumbu Y→x=0

y=0^2+3(0)-4=-4

Jadi, titik potong dengan sumbu Y adalah (0,-4).

Menentukan koordinat titik puncak y=x^2+3x-4, a=1,b=3,c=-4

x=(-b)/2a=(-3)/(2(1))=-3/2=-1 1/2

y=(-D)/4a

=-(3^2-4(1)(-4))/(4(1))

=-(9+16)/4=-25/4=-6 1/4

Jadi, koordinat titik puncaknya adalah (-1 1/2,-6 1/4).

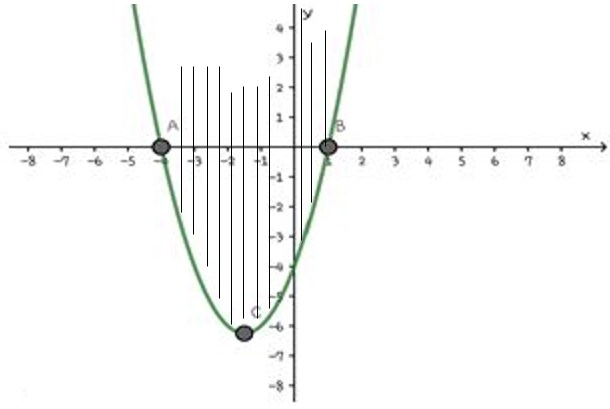
2. Uji titik

Ambil titik uji P(0,0) diperoleh:

0≥0^2+3(0)-4⇔0≥-4

Jadi, daerah himpunan penyelesaian pertidaksamaan y=x^2+3x-4 adalah belahan bidang yang memuat titik P(0,0).

 

2. Sistem Pertidaksamaan Linear-Kuadrat

Sistem pertidaksamaan linear-kuadrat adalah sistem pertidaksamaan yang terbentuk dari dua atau lebih pertidaksamaan. Bentuk umum sistem pertidaksamaan linear-kuadrat adalah:

dengan (*) adalah tanda pertidaksamaan.

Contoh Soal dan Alternatif Penyelesaian Sistem Pertidaksamaan Linear-Kuadrat

Gambarlah grafik himpunan penyelesaian dari sistem pertidaksamaan linear-kuadrat berikut!

Alternatif Penyelesaian

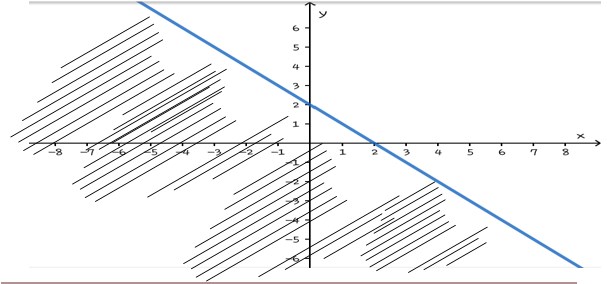
y=-x^2+x+6 merupakan parabola dengan a=-1,b=1, dan c=6. Daerah penyelesaian sistem pertidaksamaannya sebagai berikut.

y=-x+2 merupakan garis lurus yang memotong sumbu X di (2,0) dan memotong sumbu Y di (0,2).

Grafik himpunan penyelesaiannya merupakan irisan dari grafik-grafik himpunan penyelesaian pertidaksamaan-pertidaksamaan yang membentuk sistem pertidaksamaan linear-kuadrat dua variabel tersebut.

y≤-x^2+x+6;y≤-x+2

3. Sistem Pertidaksamaan Kuadrat-Kuadrat

Agar lebih mudah memahami tentang sistem pertidaksamaan kuadrat-kuadrat dua variabel, perhatikan masalah berikut!

Masalah dan Alternatif Penyelesaian Sistem Pertidaksamaan Kuadrat-Kuadrat

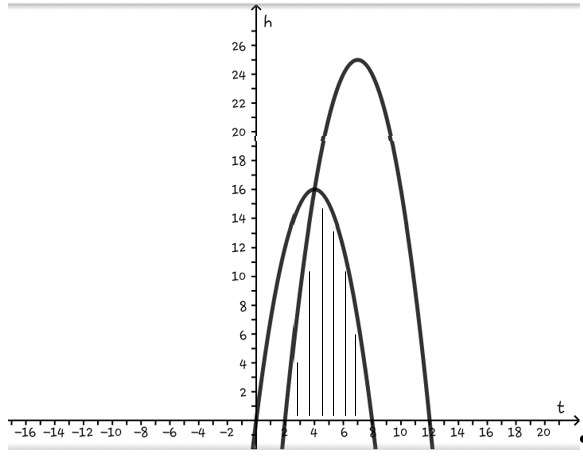
Dio akan melemparkan bola dan menginginkan ketinggian bolanya paling tidak mencapai 8t-t². Indra akan melempar bola 2 detik setelah Dio dan menginginkan ketinggian bolanya paling tidak mencapai 10t-t² (t dalam detik). Pada detik keberapa bola Dio dan bola Indra akan berada pada ketinggian yang sama? Berapa ketinggiannya?

Alternatif Penyelesaian Sistem Pertidaksamaan Kuadrat-Kuadrat

Untuk menjawab masalah diatas dibuat model matematika terlebih dahulu, misalnya

h₁ = Ketinggian bola Dio

h₂ = Ketinggian bola Indra

Menentukan pertidaksamaan untuk ketinggian masing-asing bola.

h₁ ≤ 8t-t2

Bola indra dilempar 2 detik setelah bola Dio,maka:

h₂ ≤ 10(t-2) – (t-2)2↔ h₂ ≤ 10t-20 – (t2 – 4t + 4)

h₂ ≤ 10t-20 – t2 + 4t – 4

h₂ ≤ – t2 + 14t – 24

Ketinggian tidak boleh nol, maka h₁ ≥ 0 dan h₂ ≥ 0

Sistem pertidaksamaan yang menyatakan ketinggian dari kedua bola pada waktu (t) yang bersamaan adalah:

Dengan h₁ ≥ 0 dan h₂ ≥ 0

Langkah selanjutnya adalah menggambar grafik h₁ = -t2 + 8t, kemudian menggambar grafik

h₂ = -t2 + 14t – 24

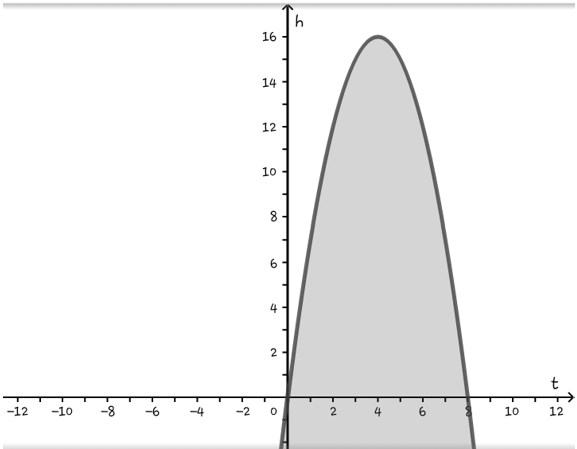
1. Menggambar grafik h₁ = -t2 + 8t

1. h1 = -t2 + 8t merupakan parabola yang mempunyai nilai a = -1 ,b = 8 dan c = 0. a = -1 , maka parabola terbuka kebawah.
2. Titik potong dengan sumbu t.
   h = 0↔-t2 + 8t = 0
   ↔t (-t + 8) = 0
   ↔t = 0 atau t = 8.
   Jadi , titik potong grafik h1 = -t2 + 8 dengan sumu t adalah (0,0) dan (8,0).
3. 
4. Uji titik untuk menentukan daerah pertidaksamaan. Ambil sembarang titik dibawah kurva, misalkan (1,0). Subtitusikan pada pertidaksamaan h₁ ≤ -t2 + 8t diperoleh 0 < 7. Jadi daerah pertidaksamaan h₁ ≤ -t2 + 8t berada dibawah kurva h₁ = -t2 + 8t. Karena h₁ ≥ 0 , maka diperoleh daerah penyelesaian seperti diatas.
5. 

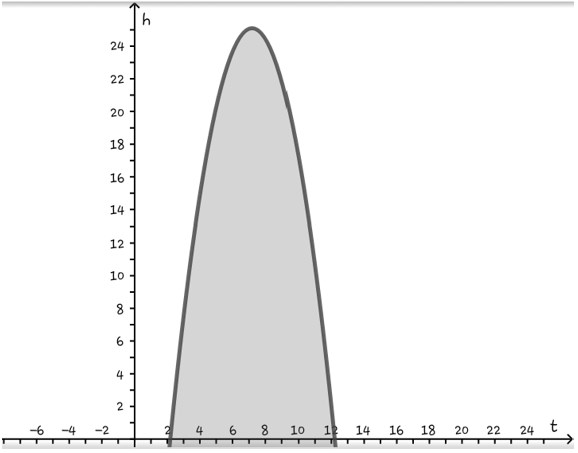
2. Menggambar grafik h2 = -t2 + 14t – 24.
   h2 = -t2 + 14t – 24 merupakan parabola yang mempunyai nilai a = -1 ,b = 14 dan c = -24.
   a = -1, maka parabola terbuka ke bawah.
   Titik potong dengan sumbu t.
   h = 0↔- t2 + 14t – 24 = 0
   ↔ t2 – 14t + 24 = 0
   ↔(t – 2) (t – 12)= 0
   ↔t = 2 atau t = 12.

Jadi, titik potong dengan sumbu t adalah (2,0) dan (12,0).

Koordinat titik puncak (-b/2a,-D/4a) = (7,25)

Uji titik untuk menentukan daerah pertidaksamaan.

Ambil sembarang titik dibawah kurva, misalkan (5,0). Subtitusikan pada pertidaksamaan h₂ ≤ -t2 + 14t – 24 diperoleh 0 < 21. Jadi, daerah pertidaksamaan h₂ ≤ -t2 + 14t – 24 berada dibawah kurva h₂ = -t2 + 14t – 24. Karena h₂ ≥ 0, maka diperoleh daerah penyelesaian seperti dibawah.

Langkah selanjutnya adalah menggabungkan kedua kuadrat grafik dalam satu sistem koordinat cartesius seperti gambar dibawah.

Diperoleh daerah himpunan penyelesaian dari sistem pertidaksamaan tersebut yang merupakan irisan dari masing-masing daerah himpunan penyelesaian pertidaksamaan kuadrat yang membentuknya.

Sistem pertidaksamaan kuadrat dua variabel adalah sistem pertidaksamaan yang terbentuk dari dua atau lebih pertidaksamaan kuadrat dua variabel dengan variabel-variabel yang sama, misalnya:

Daerah atau grafik himpunan penyelesaian dari sistem pertidaksamaan kuadrat dua variabel merupakan irisan dari masing-masing daerah himpunan penyelesaian pertidaksamaan kuadrat yang membentuknya.

Contoh Soal dan Alternatif Penyelesaian Sistem Pertidaksamaan Kuadrat-Kuadrat

Gambarlah grafik himpunan penyelesaian dari sistem pertidaksamaan kuadrat dua variabel berikut!

Alternatif Penyelesaian Sistem Pertidaksamaan Kuadrat-Kuadrat

Pertama digambarkan masing-masing grafik himpunan penyelesaian dari pertidaksamaan-pertidaksamaan yang membentuk sistem pertidaksamaan tersebut.

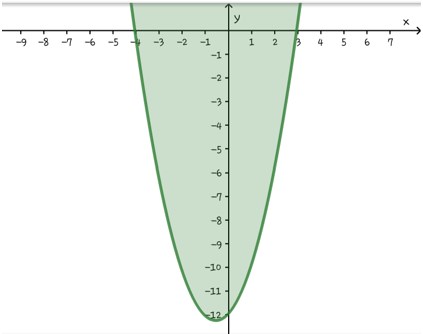
y=x^²+x-12 merupakan parabola dengan a=-1,b=1, dan c=-12. Daerah penyelesaian sistem pertidaksamaannya sebagai berikut.

y=x^²+x-12

y=-x^²+4x+12 merupakan parabola dengan a=-1,b=4, dan c=12. Daerah penyelesaian sistem pertidaksamaannya sebagai berikut.

Grafik himpunan penyelesaiannya merupakan irisan dari grafik-grafik himpunan penyelesaian pertidaksamaan-pertidaksamaan yang membentuk sistem pertidaksamaan kuadrat dua variabel tersebut.